2020 год № 4

Резюме:

Ключевые слова:

Summary:

Key words:

Введение

Недавно вошедший в исследовательскую практику фрактальный математический анализ - практически единственный метод, дающий возможность количественно измерять параметры хаотических процессов, повсеместно распространенных в природе.

Термин "фрактал" в середине 20 века ввел в научный лексикон математик Бенуа Мандельброт, определивший его как структуру, состоящую из частей, определенным образом подобных целому. Он проиллюстрировал свое математическое видение фрактала специальными изображениями фигур с рекурсивным изменением каждого их сегмента, сделанными с помощью компьютера [6]. При наблюдении фрактальных объектов в разных масштабах измерений можно видеть, что они проявляют себя фигурой, которая повторяется на разных уровнях (рисунок).

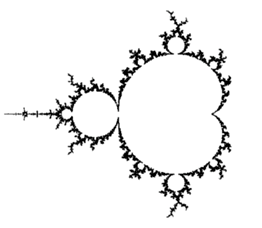
Рис. Классический фрактал: граница множества Мандельброта

Фрактальный объект может выглядеть совершенно одинаково независимо от того, наблюдается ли он в метровом, миллиметровом или микронном масштабе.

Результаты и обсуждение

Наглядным примером фрактальной структуры, например, является папоротник, каждая часть которого в увеличенном виде воспроизводит целое растение. Все фракталы имеют внутреннее свойство подобия (самоподобия) на разных уровнях [14, 25, 36, 37, 38, 52]. Самоподобие системы означает, что структура или процесс выглядят одинаково в разных масштабах или в различных по продолжительности интервалах времени. Биологические системы, как известно, часто соответствуют самоподобным свойствам организации и функционирования хаотических процессов, единственным способом количественного изучения которых является фрактальный анализ [6, 37, 38]. Так, на кривой частоты сердечных сокращений, записанной на протяжении нескольких часов, можно найти быстрые флуктуации, диапазон и последовательность которых похожи на соответствующие характеристики исходного графика. На более короткой кривой кардиоинтервалов можно обнаружить быстрые флуктуации, которые напоминают колебания на исходном графике и выглядят самоподобными, как ветви геометрического фрактала. То есть, сердечный ритм, как правило, представляет собой типичную фрактальную структуру и может быть адекватно описан методами фрактального анализа.

Структуры организма человека и животных имеют сложную пространственную организацию, которую невозможно оценить традиционными морфометрическими методами. Такие объекты с разветвленной структурой считают квазифрактальными, т. е. по свойствам приближенными к фракталам [6, 68]. Исследователи давно обратили внимание на наличие в организме животных и людей большого количества фракталоподобных образований [6, 36, 49]. Часть авторов считает, что фрактальность является одним из основных свойств строения живой природы, в частности, потому, что все биологические фракталоподобные структуры просты для генетического кодирования и основной биологический механизм разветвления может быть многократно повторен. Такая генетическая реитерация обеспечивает тем самым хорошую воспроизводимость генетической информации [2, 3, 50, 68].

Считается, что для сложных биологических объектов фрактальные показатели более корректно описывают форму объекта, чем традиционно используемые в морфометрии критерии, основанные на принципах эвклидовой геометрии [26, 43, 49, 52].

Наиболее часто используемыми параметрами, харак­теризующими квазифрактальную систему со сложным хаотическим состоянием, являются:

H - показатель Херста, характеризующий модность системы;

D - фрактальная размерность - показатель сложности кривой, указывающий на количество факторов, влияющих на систему - индикатор состояния кризиса и нестабильности;

Ae - показатель аппроксимации энтропии;

Le - индекс Ляпунова - показатель, характеризующий степень расходимости изначально близких траекторий [6, 68].

С развитием вычислительной техники появилась возможность оперативно анализировать фрактальные свойства биологических структур, что нашло применение, в частности, в области медицины, животноводства, пищевой промышленности. В качестве примера можно привести опубликованный информативный сравнительный анализ гистоструктуры мышечной и жировой ткани свинины и говядины различных пород из разных стран с использованием параметров фрактальной размерности (FD) и box counting алгоритма [2, 4, 19, 22, 23, 24, 64].

Анализ фрактальных свойств биологических структур позволил разработать новые модели для изучения тех или иных органов или систем организма человека. Например, создано несколько фрактальных моделей кровообращения in vitro [32, 42, 61]. Вид моделей - разветвленная "древовидная" структура. Процессы обмена веществ на уровне микро-циркуляторного русла описываются согласно теории инвазивной перколяции (протекания), изучаемой в модели капилляров, когда определяется и отображается пороговое давление каждого звена, и кровь начинает течь из одного звена русла в другое ("ветви дерева") [42].

Фрактальный анализ применяют для исследования белого и серого вещества головного мозга, его сосудистой сети, отдельных нейронов, [12, 31, 62, 71]. К квазифрактальным структурам относят мозжечок человека, его разветвленные белое вещество и кора. Исследована трехмерная фрактальная размерность скелетированного белого вещества мозжечка [48], определены трехмерные индексы его белого и серого вещества в норме и при патологии [15, 69].

Перспективность применения фрактального анализа структуры и функции органов и тканей для диагностики и прогноза развития ряда патологических состояний не вызывает сомнений [26, 34, 39, 50].

Оценка фрактальных характеристик стала эффективным инструментом количественного анализа сложных медицинских изображений [20].

В частности, фрактальный анализ используют для диагностики опухолевого процесса; оценки ангиогенеза и распределения коллагена в тканях; при исследованиях патологии печени, селезенки, поджелудочной железы, почек, кожи, для анализа нейрональных и глиальных изменений в головном мозге при различных функциональных и патологических состояниях на тканевом, клеточном и субклеточном уровнях. Достигнуты первые практические результаты [7, 18, 26, 27, 39, 40, 49, 67].

В частности, установленные фрактальные параметры фиброза печени имеют достаточно высокий уровень диагностической точности и хорошую воспроизводимость [27, 33, 46, 54]. F. Моаі с соавторами утверждают, что фрактальный анализ - единственный количественный метод оценки морфологической структуры, позволяющий различать фиброз различного происхождения, в том числе, изменения, вызванные действием фармакологических веществ [54].

В работах ряда авторов методы фрактального анализа используются для распознавания патологических процессов в молочных железах на основании данных термографии [17, 29, 30, 60]. Авторы выделяют участки поверхности с наибольшей температурой и анализируют их контуры, рассчитывая фрактальную размерность [30]. Показано, что для доброкачественных опухолей фрактальная размерность контуров составляет 1,04±0,07, для злокачественных - 1,33±0,04 (р<0,01), т. е. контуры злокачественной опухоли более иррегулярны, чем доброкачественной. В целом, злокачественное новообразование определяется как хаотическая, слабо регулируемая структура, плохо описываемая евклидовой геометрией [17]. Поэтому для дифференциальной диагностики доброкачественных и злокачественных опухолей по маммографическим изображениям предложен анализ мультифрактального спектра (Multifractal Spectrum Analysis) - метод оценки параметров локальной регулярности [29].

В последние годы исследователи все больше внимания уделяют изучению фрактальной организации на уровне сосудистого русла [1, 47, 51]. В частности, при анализе ретинопатий различного генеза показано значимые изменения фрактальной размерности D микроциркуляторного русла сетчатки глаза человека по сравнению со здоровой сетчаткой [13, 53, 56].

Считается, что для анализа микроциркуляторного русла лучше всего подходит именно показатель фрактальной размерности D, который характеризуется высокой робастностью (устойчивостью к влиянию на результат различного рода "выбросов", выбивающихся из графика точек) и повторяемостью [51]. Изменения фрактальных показателей микроциркуляторного русла могут быть вызваны значительным уменьшением или увеличением диаметров сосудов, их количества и изменением геометрии разветвления в процессе ангиогенеза, что часто наблюдается при некротических или онкологических перерождениях тканей. Е. Gaudio с соавторами указывают на значительную разницу фрактальных показателей синусоидального русла при моделировании различных видов цирроза печени [33]. То же явление наблюдалось на сосудистом уровне при моделировании in vivo различных видов цирроза у крыс [10, 57].

Оценивая использование фрактального морфометрического анализа для диагностики, следует отметить, что большинство исследований было проведено на гистологических препаратах. В последние годы для фрактального анализа сосудистого русла начали использовать данные ретиноскопии, MRT и компьютерной томографии [45, 50, 56].

К настоящему времени разработано значительное количество нелинейных динамических оценок временных рядов сложных биологических систем, в частности, сердечного ритма (СР).

После открытия Э. Голдбергером с соавторами в 1980-х годах фракталоподобности временных параметров сердечной активности [35, 36, 37] были попытки разработать дополнительные диагностические комплексы, полезные для изучения переходных состояний, которые не поддаются анализу с использованием стандартных методов оценки вариабельности сердечного ритма (ВСР) [16, 21]. Было предложено несколько вариантов расчета фрактальных показателей на коротких рядах R-R интервалов [5, 16, 66]. Фрактальный анализ ВСР был использован для выявления нарушений в физиологических системах у беременных женщин, обнаружения риска внезапной смерти, онкологических заболеваний, уровня утомления и эффективности работы регуляторных систем при физических тренировках [8, 9, 11, 63]. Сделаны отдельные попытки изучения аномалий сердечного ритма с использованием фрактального анализа, в частности, по параметрам фрактальной размерности и энтропии [41, 55, 70]

Все вышеизложенное позволяет считать фрактальный анализ весьма перспективным методом для решения большого спектра общебиологических и медицинских исследовательских задач.

Литература

1. 1. Гелашвили О.А. Фракталоподобная организация формирующегося гемомикроциркуляторного русла мышц человека // Морфология. - 2006. - № 130 (5). - С. 35.
2. 2. Жегунов Г.Ф. Законы биологии. Природа жизни. - Харьков: Консум, 2006. - 304 с.
3. 3. Исаева В.В., Каретин Ю.А., Чернышев А.В., Шкуратов Д.Ю. Фракталы и хаос в биологическом морфогенезе. - Владивосток: Институт биологии моря ДВО РАН, 2004. - 128 с.
4. 4. Лихач В.Я., Лихач А.В., Шебанин П.А. Гистологическое строение мышечной ткани свиней различных пород и сочетаний в условиях промышленной технологии // Инновации и продовольственная безопасность. - 2015. - № 1 (7). - С. 31-37.
5. 5. Майоров О.Ю., Фенченко В.Н. Применение локального индекса фрактальности для анализа коротких рядов R-R интервалов при исследовании вариабельности сердечного ритма // Клиническая информатика и телемедицина. - 2010. - № 6 (7). - 6-12.
6. 6. Мандельброт Б. Фрактальная геометрия природы / Б. Мандельброт. - М.: Институт компьютерных исследований, 2002. - 656 с.
7. 7. Марченко В.С., Бабийчук Г.А., Грищенко В.И., Бабийчук В.Г. К концепции экзистоэнцефалической системы охлажденного мозга. Часть 4. Фрактальная морфометрия триггерных структур терморегуляции при холодовом стрессе // Проблемы криобиологии. - 2002. - № 4. - С. 30-40.
8. 8. Охремчук А.П., Шмонина О.Н. Контроль функционального состояния организма занимающихся в группе здоровья с использо­ванием аппаратно-программного комплекса / Ученые записки университета им. П.Ф. Лесгафта. - СПб., 2017. - Вин. 2 (144). - С. 168-173.
9. 9. Рахимов Н.Г., Олимзода Н.Х., Давлятова Г.К., Мурадов А.М., Мурадов А.А. Фрактальная оценка и вариабельность сердечного ритма у беременных с тяжёлой преэклампсией и эклампсией в третьем триместре // Вестник последипломного образования в сфере здравоохранения. - Душанбе, 2017. - № 1. - С. 61-65.
10. 10. Слета И.В., Чиж Н.А., Луценко Д.Г., Белочкина И.В., Олефиренко А.А., Сандомирский Б.П. Криохирургия при диффузных заболеваниях печени // Клиническая хирургия. - 2010. - № 6. - № 27-33.
11. 11. Яцык В.З., Парамзин В.Д., Болотин А.Э., Воротова М.С. Фрактальный анализ вариабельности сердечного ритма у биатлонисток с разным уровнем тренированности // Физиология. - 2018. - Вып. 4. - С. 95-102.
12. 12. De Luca, F. Arrigoni, R. Romaniello [et al.] Automatic localization of cerebral cortical malformations using fractal analysis // Phys. Med. Biol. - 2016. - Vol. 61 (16). - P. 6025-6040.
13. 13. Ab Hamid F., CheAzemin M.Z., Salam A., Aminuddin A., MohdDaud N., Zahari I. Retinal vasculature fractal dimension measures vessel density // Curr Eye Res. - 2016. - № 41 (6). - Р. 823-831.
14. 14. Adrien Depeursinge, Omar S Al-Kadi, J. Ross Mitchell. Biomedical Texture Analysis: Fundamentals, Tools and Challenges. - London: Academic Press, 2017. - 430 p.
15. 15. Akar E., Kara S., Akdemir H., Kiris A. Fractal analysis of MR images in patients with Chiari malformation: The importance of preprocessing // Biomedical Signal Processing and Control. - 2017. - № 31. - P. 63-70.
16. 16. Aubert A.E., Vandeput S., Beckers F., Liu J., Verheyden B., Van Huffel S. Complexity of cardiovascular regulation in small animals // Philos Trans A Math Phys Eng Sci. - 2009. - № 367 (1892). - Р. 1239-1250.
17. 17. Baish J. W., Jain R. K. Fractals and cancer // Cancer Res. - 2000. - Vol. 60. - P. 3683-3688.
18. 18. Balay-Karperien A. Defining Microglial Morphology: Form, Function, and Fractal Dimension: thesis for the degree of Master of health science (honours) research // Melbourne: Charles Sturt University. - 2004. - 246 p.
19. 19. Bianciardi G., Buonsanti M., Pontari A., et al. Fractal analysis and biophysical investigation of muscular tissue damaged due to low temperature: a pilot study // Journal of Biomimetics, Biomaterials and Tissue Engineering. - 2012. - Vol. 14. - P. 43-51.
20. 20. Bubnov R.V., Melnyk I.M. The methods of fractal analysis of diagnostic images. Initial clinical experience. - 2011. - № 3-4. - P. 108-113.
21. 21. Captur G., Karperien A.L., Hughes A.D., Francis D.P., Moon J.C. The fractal heart - embracing mathematics in the cardiology clinic // Nat Rev Cardiol. - 2017. - № 14 (1). - 56-64.
22. 22. Chang R., Wei Y., Ma L., et al. The judgment of beef marble texture based on the MATLAB image pro­cessing technology / International Conference on Computer and Computing Technologies in Agriculture (Nanchang, October 22-25, 2010). - Berlin, Heidelberg: Springer, 2010. - P. 106-112.
23. 23. Chen J., Liu M., Zong L. The fractal dimension research of Chinese and American beef mar­bling standards images / International Conference on Com­puter and Computing Technologies in Agriculture (Zhangjiajie, October 19-21, 2012). - Berlin, Heidelberg: Springer, 2012. - P. 199-209.
24. 24. Chen К., Qin C. Fractal feature analysis of beef marbling patterns / International Conference on Computer and Computing Technologies in Agriculture (Beijing, October 18-20, 2008). - Boston (MA): Springer, 2008. - P. 2177-2186.
25. 25. Delignières, D., & Torre, K. Fractal dynamics of human gait: a reassessment of the 1996 data of Hausdorff, et al. // Journal of Applied Physiology. - 2009. - № 106 (4). - Р. 1272-1279.
26. 26. Dey P. Basic principles and applications of fractal geometry in pathology: a review // Anal Quant CytolHistol. - 2005. - Р. 27 (5). - Р. 284-90.
27. 27. Dioguardi N., Grizzi F., Franceschini B., Bossi P., Russo C. Liver fibrosis and tissue architectural change measurement using fractal-rectified metrics and Hurst's exponent // World J Gastroenterol. - 2006. - № 12 (14). - Р. 2187-94.
28. 28. Dobrykh V.A., Kashina T.V., Ten T.K., Uvarova I.V., Sedakov V.O. The experience of studying of heart rate variability by methods of fractal analysis and nonlinear dynamics in healthy men // Актуальные направления фундаментальных и прикладных исследований: Материалы XVIII международной научно-практической конференции. - 2019. - С. 20-22.
29. 29. Dumansky Y.V, Lyakh Y.E., Gorshkov O.G., Gurianov V.G., Prihodchenko V.V. Fractal dimensionality analysis of normal and cancerous mammary gland thermograms // Chaos, Solitons and Fractals. - 2012. - Vol. 45. - P. 1494-1500.
30. 30. Etehadtavakol M., Lucas C., Sadri S., Ng E.Y.K. Analysis of breast thermography using fractal dimension to establish possible difference between malignant and benign patterns // J. Healthcare Eng. - 2010. - Vol. 1, № 1. - P. 27-43.
31. 31. Farahibozorg S., Hashemi-Golpayegani S. M., Ashburner J. Age- and sex-related variations in the brain white matter fractal dimension throughout adulthood: an MRI study/ Clin. Neuroradiol. - 2015. - Vol. 25 (1). - P. 19-32.
32. 32. Gabrys E., Rybaczuk M., Kedzia A. Blood flow simulation through fractal models of circulatory system / Chaos, Solitions and Fractals. - 2006. - Vol. 27. - P. 1-7.
33. 33. Gaudio E., Chaberek S., Montella A., Pannarale L., Morini S., Novelli G., Borghese F., Conte D., Ostrowski K. Fractal and Fourier analysis of the hepatic sinusoidal network in normal and cirrhotic rat liver // J Anat. - 2005. - № 207 (2). - Р. 107-115.
34. 34. Glenny R.W., Robertson H.T., Yamashiro S., Bassingthwaighte J.B. Applications of fractal analysis to physiology // J Appl Physiol. - 1991. - № 70 (6). - Р. 2351-2367.
35. 35. Goldberger A.L., Findley L., Blackburn M.J., Mandell A.J. Nonlinear dynamics of heart failure: implications of long-wavelength cardiopulmonary oscillations // Am Heart J. - 1984. - № 107 (3). - Р. 612-615.
36. 36. Goldberger A.L., Rigney D.R., West B.J. Chaos and fractals in human physiology // Sci Am. - 1990. - № 262 (2). - Р. 42-49.
37. 37. Goldberger A.L., West B.J. Fractals in physiology and medicine // Yale J Biol Med. - 1987. - № 60 (5). - Р. 421-35.
38. 38. Hausdorff J.M., Purdon P.L., Peng C.K., Ladin Z., Wei J.Y., Goldberger A.R. Fractal dynamics of human gait: stability of long-range correlations instride interval fluctuation // J Appl Physiol. - 1996. - № 80. - Р. 1448-1457.
39. 39. Heymans O., Fissette J., Vico P., Blacher S., Masset D., Brouers F. Is fractal geometry useful in medicine and biomedical sciences? // Med Hypotheses. - 2000. - № 54 (3). - Р. 360-366.
40. 40. Hinwood M., Tynan R.J., Charnley J.L., Beynon S.B., Day T.A., Walker F.R. Chronic stress induced remodeling of the prefrontal cortex: structural re-organization of microglia and the inhibitory effect of minocycline // Cereb Cortex. - 2013. - № 23 (8). - Р. 1784-1797.
41. 41. Hou Z., Li F.W., Wang J., Yan F.R. Visibility graph analysis of very short-term heart rate variability during sleep // Physica A: Statistical Mechanics and its Applications. - 2016. - Vol. 458. - P. 140-145.
42. 42. Jayalalitha G., ShantoshiniDeviha V., Uthayakumar R. Fractal model for blood flow in cardiovascular system // Computers in Biology and Medicine. - 2008. - Vol. 38. - P. 684-693.
43. 43. Karperien A., Ahammer H., Jelinek H.F. Quantitating the subtleties of microglial morphology with fractal analysis // Front Cell Neurosci. - 2013. Jan 30. - № 7. - Р. 3.
44. 44. Karperien A.L., Jelinek H.F., Buchan A.M. Box- counting analysis of microglia form in schizophrenia, Alzheimer's disease and affective disorder // Fractals. - 2008. - № 16 (2). - Р. 103-117.
45. 45. Karperien A.L., Jelinek H.F. Box-Counting Fractal Analysis: A Primer for the Clinician. In: Di Ieva A, editor. The Fractal Geometry of the Brain. - New York: Springer, 2016. - P. 13-44.
46. 46. Landini G., Iannaccone P.M. Modeling of mosaic patterns in chimeric liver and adrenal cortex: algorithmic organogenesis? // FASEB J. - 2000. - № 14 (5). - Р. 823-827.
47. 47. Lapi D., Marchiafava P.L., Colantuoni A. Geometric characteristics of arterial network of rat pial microcirculation // J Vasc Res. - 2008. - № 45 (1). - Р. 69-77.
48. 48. Liu J.Z. Fractal dimension in human cerebellum measured by magnetic resonance imaging / J.Z. Liu, L.D. Zhang, G.H. Yue // Biophys. J. - 2003. - Vol. 85 (6). - P. 4041-4046.
49. 49. Losa G.A. The fractal geometry of life // Riv Biol. - 2009. - № 102 (1). - Р. 29-59.
50. 50. Losa GA. On the Fractal Design in Human Brain and Nervous // Tissue. Appl Math. - 2014. - № 5. - 1725-1732.
51. 51. Mancardi D., Varetto G., Bucci E., Maniero F., Guiot C. Fractal parameters and vascular networks: facts & artifacts // TheorBiol Med Model. - 2008. - Jul. 17. - № 5. - Р. 12.
52. 52. Manuel Varela, Raul Ruiz-Esteban, and Maria Jose Mestre De Juan Chaos, Fractals, and Our Concept of Disease // Perspectives in Biology and Medicine. - Vol. 53, № 4, Autumn 2010. - P. 584-595.
53. 53. Masters BR. Fractal analysis of the vascular tree in the human retina // Annu Rev Biomed Eng. - 2004. - № 6. - Р. 427-52.
54. 54. Moal F., Chappard D., Wang J., Vuillemin E., Michalak-Provost S., Rousselet M.C., Oberti F., Calès P. Fractal dimension can distinguish models and pharmacologic changes in liver fibrosis in rats // Hepatology. - 2002. - № 36 (4 Pt 1). - Р. 840-849.
55. 55. Mondejar-Guerra V., Novo J., Roucoab J., Penedo M.G., Ortega M. Heartbeat classification fusing temporal and morphological information of ECGs via ensemble of classifiers // Biomedical Signal Processing and Control. - 2019. - Vol. 47. - P. 41-48.
56. 56. Nagaoka T., Yoshida A. Relationship between retinal fractal dimensions and retinal circulation in patients with type 2 diabetes mellitus // Curr Eye Res. - 2013. - № 38 (11). - 1148-52.
57. 57. Olefirenko A.A., Lutsenko D.G., Sleta I.V., Marchenko V.S. Use of fractal analysis for evaluation of liver structure and function in rats in vivo // Bull Exp Biol Med. - 2009. - № 147 (2). - Р. 273-276.
58. 58. Pantic I., Nesic D., Stevanovic D., Starcevic V., Pantic S., Trajkovic V. Effects of Ghrelin on the structural complexity of exocrine pancreas tissue architecture // Microsc Microanal. - 2013. - № 19 (3). - Р. 553-538.
59. 59. Pantic I., Paunovic J., Basta-Jovanovic G., Perovic M., Pantic S., Milosevic N.T. Age-related reduction of structural complexity in spleen hematopoietic tissue architecture in mice // ExpGerontol. - 2013. - № 48 (9). - 926-932.
60. 60. Ramirez-Cobo P., Vidakovic B. A 2D wavelet-based multiscale approach with applications to the analysis of digital mammograms // Computational Statistics and Data Analysis. - 2013. - Vol. 58, № 2. - P. 71-81.
61. 61. Reymond P., Merenda P., Perren F. et al. Validation of a one-dimensional model of the systemic arterial tree // American Journal of Heart and Circulatory Physiology. - 2009. - Vol. 297 (1). - P. 202-228.
62. 62. Ristanovic D., Stefanovic B. D., Puskas N. Fractal analysis of dendrite morphology using modified box-counting method // Neurosci. Res. - 2014. - Vol. 84. - P. 64-67.
63. 63. Sen Jonathan, Darry McGill Fractal analysis of heart rate variability as a predictor of mortality: A systematic review and meta-analysis / Chaos: An Interdisciplinary Journal of Nonlinear Science. - 2018. - Volume 28, Issue 7.
64. 64. Serrano S., Peran F., Jimenez-Homero F.J., et al. Multifractal analysis application to the characterization of fatty infiltration in Iberian and White pork sirloins // Meat science. - 2013. - Vol. 93 (3). - P. 723-732.
65. 65. Tsvetkov V.P., Mikheyev S.A., Tsvetkov I.V. Fractal phase space and fractal entropy of instantaneous cardiac rhythm / Chaos, Solitons & Fractals. - 2018. - Vol. 108. - P. 71-76.
66. 66. Tulppo M.P., Kiviniemi A.M., Hautala A.J., Kallio M., Seppänen T., Mäkikallio T.H., Huikuri H.V. Physiological background of the loss of fractal heart rate dynamics // Circulation. - 2005. - № 112 (3). - Р. 314-319.
67. 67. Waliszewski P., Wagenlehner F., Gattenlöhner S., Weidner W. Fractal geometry in the objective grading of prostate carcinoma // Urologe A. - 2014. - № 53 (8). - Р. 1186-1194.
68. 68. Weibel E.R. Fractal geometry: a design principle for living organisms // Am J Physiol. - 1991. - № 261 (6 Pt 1). - Р. 361-369.
69. 69. Wu Y.T., Shyu K.K., Jao C.W. [et al.] Fractal dimension analysis for quantifying cerebellar morphological change of multiple system atrophy of the cerebellar type (MSA-C) // Neuroimage. - 2010. - Vol. 49 (1). - P. 539-551.
70. 70. Yalcin Isler, Ali Narin, Mahmut Ozer, MatjazPerc. Multi-stage classification of congestive heart failure based on short-term heart rate variability // Chaos, Solitons & Fractals. - 2019. - Vol. 118. - P. 145-151.
71. 71. Zaletel I., Ristanovic D., Stefanovic B.D. Modified Richardson's method versus the box-counting method in neuroscience // J. Neurosci. Methods. - 2015. - Vol. 242. - P. 93-96.